We want to use GSP to construct a parabola.

In Assignments 2 and 3 we looked at the parabola from the viewpoint of the quadratic equation, but we can also notice what exactly is a parabola.

A parabola is a set of points that are equidistant from a given line, which we call the directrix, and a given fixed point not on the line, called the focus.

Let's first set up this line and this point.

We want to find the set of points that are the same distance from the focus as they are from the directrix.

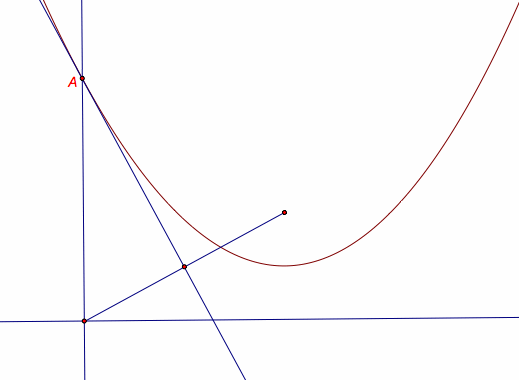
Does point A below qualify? Does distance 1 equal distance 2?

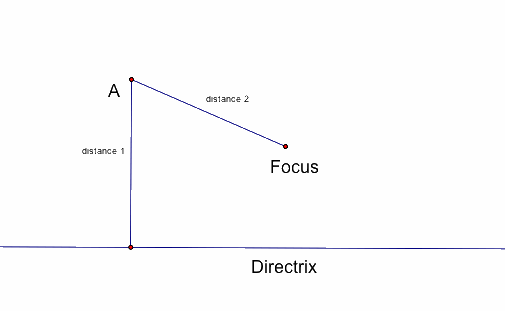
Without measuring, we cannot tell if the distance between point A and the directrix (distance 1) equals the distance between point A and the focus (distance 2).

We can, however, construct points that we know are equal distances from the focus and the directrix.

Why do we want to do this again? Remember, these points will make up a parabola! Once we find these points, we will have a parabola!

How do we do find these points? Follow below.

First, take any point on the directrix, construct a segment from the focus to this point, and find the midpoint of this segment.

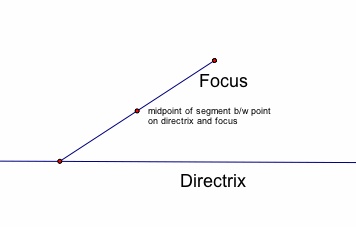
Next, construct the perpendicular line to this midpoint and segment.

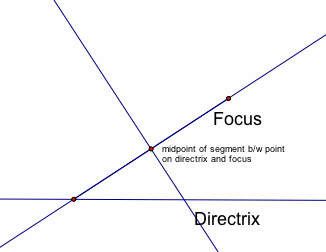
Then, construct the perpendicular to the directrix at the point identified on the directrix. Find the point of intersection of these two perpendicular lines.

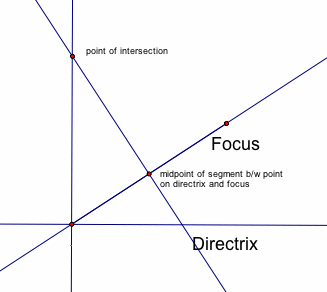
Notice, this point of intersection is equidistant to the focus and the directrix. Why?

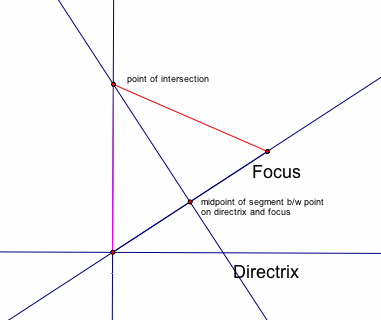
We want to show that the red line is equal to the magenta line above. Let's think about this.

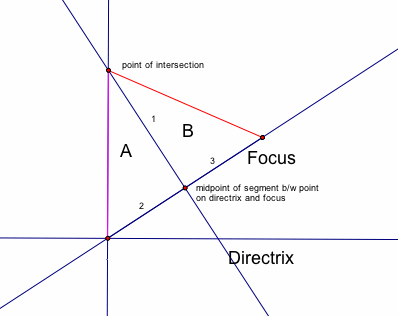
We have two right triangles, one with the magenta hypotenuse- triangle A, and one with the red hypotenuse-triangle B.

The two legs of triangle A are side 1 and side 2. The two legs of triangle B are side 1 and side 3. Because we constructed the midpoint of the segment side 2 and side 3 lie on, side 2= side 3.

Because these are right triangles and the two sides of the right triangles are equal, the hypotenuses of triangle A and triangle B are equal.

What does this mean? We have constructed a point that is equidistant from the focus and the directrix! This will be a point on our parabola!

Below, the point A is our constructed point, with most of the lines we used to construct it hidden.

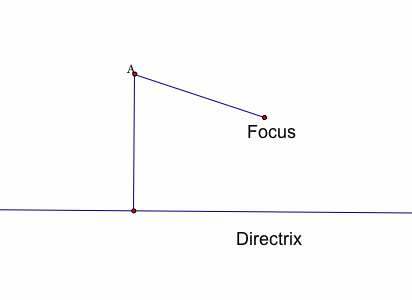
Now, we can move the point on the directrix and point A will move along with it, giving more points of the parabola!

Below, is a series of images with the point on the directrix moving along the directix. Notice how A moves along with it and the distance between A and the focus is always equal to the distance between A and the directrix.

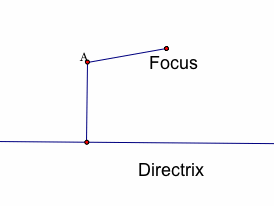
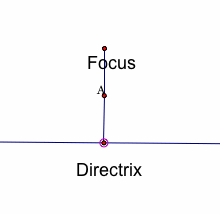
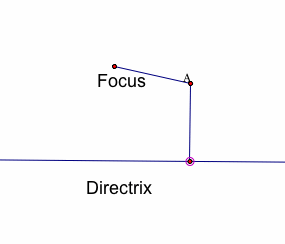
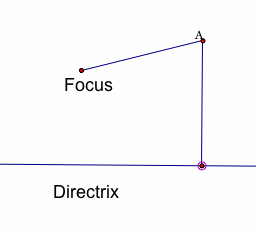
Each of the images above show point A as different points on the same parabola.

We can use GSP to animate the point on the directrix and also trace the path of point A. The trace will now, finally, give us our parabola for this fixed focus and given fixed line.

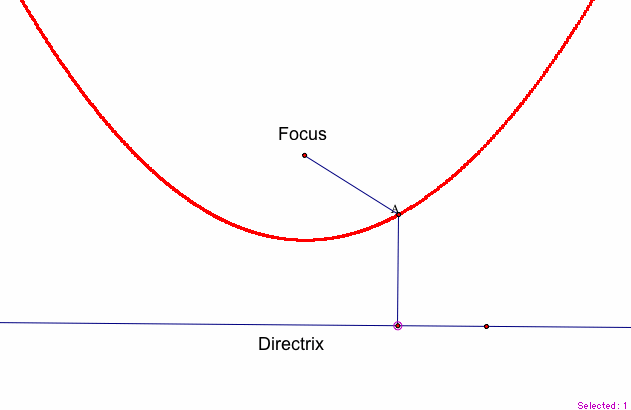
Click here for the GSP file that created our parabola above. Click Animate point B to see the point on the directrix move along the directrix and watch the trace that the point A creates- a parabola.

b. Repeat 9a with a trace of the tangent line at the constructed point.

Above, we have created a parabola by tracing the point A as the point on the directrix moves along the directrix.

Now, we can see a parabola created by tracing the tangent line rather than the actual point as the point on the directrix is moved.

The tangent line I am referring to is the line we created by forming the perpendicular to the midpoint of the line segment connecting our fixed point, the focus, and the point on the directrix.

Remember, we next created a perpendicular line with the point on the directrix and the directrix that then lead to our point of intersection A.

Before, we animated this point of intersection, but now we want to animate the line through it- the red line below.

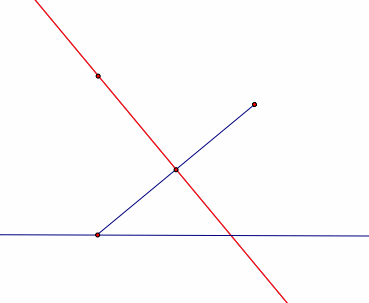
Let's animate it and see what happens.

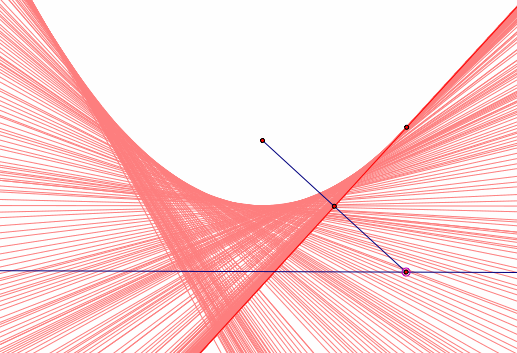
It appears that we are forming a parabola from the traces. If the trace goes all the way up and back down, we will have outlined a parabola. See below.

Click Here for the GSP file that created our parabola above. Click Animate Point B to see the animation and watch the traces form the parabola.

c. Use the locus command to generated the parabola from a constructed point or the tangent line at that point.

We can also construct the parabola by using the locus command on GSP. Since the parabola is the locus our constructed point, that we above called A. Point A, as we constructed it above, is always equidistant to the directrix and to the fixed focus point. The locus is the set of all points A. Earlier we traced the point A as a point on the directrix was animated, giving us the parabola. The locus command on GSP will directly give us the set of all points (A) that are equidistant from the directrix and the focus.

Our result can be seen below. The red parabola is the locus of the constructed point A with respect to the directrix.

Return Home